[플라네타리움 구현기] 3. 좌표계 변환

Develop, #0. 플라네타리움 구현기
  1. 1. 목차
  2. 2. 천구좌표계
    1. 2.1. 지평좌표계
    2. 2.2. 적도좌표계
    3. 2.3. 좌표계 변환
      1. 2.3.1. 항성시
      2. 2.3.2. 변환 공식
      3. 2.3.3. coordinate.js
      4. 2.3.4. debug.js
  3. 3. 결과

목차

지금까지 한 일들은 다음과 같습니다.

이제 이번 챕터에서는 핵심 로직중 하나인 좌표계 변환을 구현합니다.

코드를 설명하기 전에 간단하게 좌표계에 관한 내용을 다루고 갑시다.

천구좌표계

하늘에 있는 별들은 고정된 점이라 간주해도 됩니다. 별이 움직이기는 하지만 관측을 진행하고 있는 지구와는 상당히 멀기 때문에 움직임이 거의 보이지 않습니다.

고정된 점(혹은 별)에 위치를 주는 방법은 여러가지입니다. 같은 점을 표현할 때 직교좌표계와 극좌표계를 이용하여 두 가지 방식으로 표현할 수 있다는 점을 생각하면 좋습니다. 좌표계마다 장단점이 있지만, 두 좌표계 모두 똑같은 점을 표현합니다.

또한, 두 좌표계가 표현할 수 있는 영역이 같다면 한 좌표계의 점을 좌표계의 점으로 변환할 수 있는 공식이 존재합니다. 이 글에서 사용하고 있는 지평좌표계와 적도좌표계에 대해서 알아보고 어떻게 서로 변환할 수 있는지 알아봅시다.

지평좌표계

지평좌표계는 실제로 천체관측을 할 때 가장 직관적인 좌표입니다. 별이 어느 방향(방위각) 에서 얼마나 높이(고도) 떠있는지를 사용하여 별의 위치를 표현합니다.

지평좌표계 (Wikipedia)

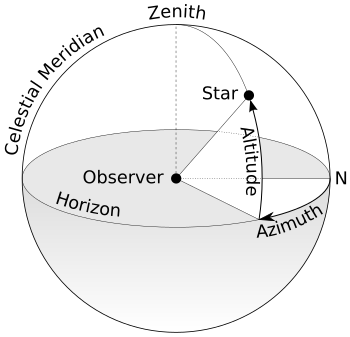
현실에서 천체관측을 할 경우 가장 확실하게 알 수 있는 방위는 북쪽입니다. 북극성은 비교적 찾기 쉬우며, 북극성을 찾아 지평선쪽으로 수직선을 내릴 경우 만나는 곳(북점이라고 합시다)이 북쪽이기 때문입니다.

북점(N)에서 시계방향으로 얼마나 회전해야 어떤 별에 도달하는지가 바로 방위각(Azimuth) 입니다. 위의 그림에서는 N에서 Azimuth글자의 A까지의 각도로 표현되어있습니다.

별이 땅에서 얼마나 높이 떠있나가 고도(Altitude) 입니다. 위의 그림에서는 Azimuth 글자의 A에서 Star까지의 각도로 표현되어있습니다.

따라서, 지평좌표계로 표현된 별의 위치를 찾기 위해서는 북점(N)에서 방위각(Azimuth)만큼 시계방향으로 회전한 후, 천정(Zenith)방향으로 고도(Altitude)만큼 올라가면 해당 별이 나옵니다.

지평좌표계의 가장 큰 문제점은 별의 좌표값이 관측지와 시간에 따라 실시간으로 변한다는 점입니다. 지평좌표계는 관측자의 입장에서 보는 좌표기 때문에 지구의 자전으로 인하여 별이 회전하는 것처럼 보이는 현상을 좌표값에 반영합니다.

이제는 적도좌표계에 대해서 알아봅시다. 시시각각 좌표값이 편한다는 지평좌표계의 문제를 적도좌표계가 해결할 수 있습니다.

적도좌표계

적도좌표계 역시 어느 방향(적경) 에서 얼마나 높이(적위) 떠있는지를 사용하여 별의 위치를 표현합니다. 지평좌표계와 다른 점은 기준점인 춘분점은 하늘에서 위치가 변하지 않는다는 것입니다. 이를 이해하기 위한 여러 개념들을 짚고 넘어갑시다.

적도좌표계 (Wikipedia)

밤하늘을 지구를 감싸고 있는 큰 공(천구)라고 가정합시다. 위 그림에서 천구는 회색 구로 표현되어있습니다. 모든 별은 거리와 상관없이 천구에 붙어있는 점입니다.

적도란 지구의 자전축에 수직인 위도 0도의 선인데, 지구의 적도(earth’s equator)를 늘려 천구에 확장할 수 있습니다. 이를 천구의 적도(celestial equator)라고 합니다. 위 그림에서 지구의 적도는 지구에 그어진 푸른 가로선, 천구의 적도는 천구에 그어진 푸르고 굵은 가로선입니다.

지구의 자전축을 위아래로 확장하면 천구와 만나는 점이 두 개가 생깁니다. 하나는 천구의 북극(north celestial pole)이고(대부분의 경우 지평좌표계의 천정(Zenith)과는 다릅니다), 하나는 천구의 남극(north celestial pole)입니다.

천구의 북극은 보통 천정과는 다릅니다. 천정(Zenith)은 관측자의 입장에서 본 머리 꼭대기이고, 천구의 북극은 지구의 자전축을 천구까지 이은 점입니다. 천구의 북극과 천정이 같아지는 경우가 있을까요? 북극에서는 천구의 북극과 천정이 일치합니다.

북극성을 천구의 북극이라 생각해도 무방합니다. 북극에서는 북극성이 90도 위(천정)에 위치하기 때문에 천정과 천구의 북극이 같아집니다.

스크롤하기 귀찮을 것 같으니 사진을 한 번 더 첨부합니다.

적도좌표계 (from Wikipedia)

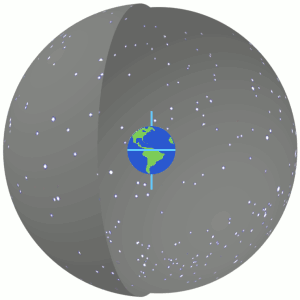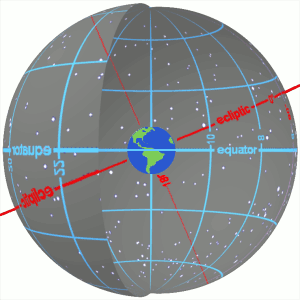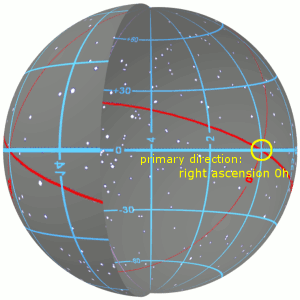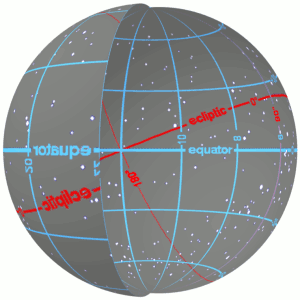
빨간색 굵은 선은 황도입니다. 1년동안 지구 입장에서 태양이 천구를 지나가는 길입니다. 해당 그림에서는 Earth’s orbital plane 이라고 표현되어 있습니다.

적도와 황도는 일치하지 않는데, 이는 지구의 자전축이 지구의 궤도와 23.5도 틀어져있기 때문입니다. 따라서 적도(푸른 굵은 선)과 황도(붉은 굵은 선)이 만나는 점에서 각도를 계산하면 23.5도가 나올 겁니다.

사진상에서 황도(붉은 선)는 반시계방향으로 진행되면서 적도와 두 번 만납니다. 만나는 두 점중에 황도가 올라가는 방향에서 만난 점을 춘분점(vernal equinox)이라고 하고 나머지 점을 추분점(autumnal equinox)이라고 합니다. 해당 그림에서 춘분점은 primary direction으로 표시된 점입니다.

적도좌표계에서 별의 위치를 표현하기 위해서는 춘분점에서 천구의 적도를 따라 어느정도 반시계방향으로 회전해야 하는지를 계산하고, 그 후 천구의 북극 방향으로 어느정도 올라가야(내려가야)하는지를 계산합니다. 앞의 값을 적경(RA, Right Ascension)이라 하고, 뒤의 값을 적위(DEC, Declination)이라 합니다.

결국 적도좌표계도 별의 위치를 표현하는 법은 비슷합니다. 하지만 기준점이 지평선의 북점이 아닌 춘분점이라는 것이 다릅니다. 위 내용을 간략하게 표현하면 다음과 같습니다.

적도좌표계 (KASI)
이제는 이 사진이 이해가 되리라 생각합니다. 지평좌표계와 비슷하게 별의 좌표를 얻지만, 기준점과 회전방향이 다르다고 생각하면 됩니다.

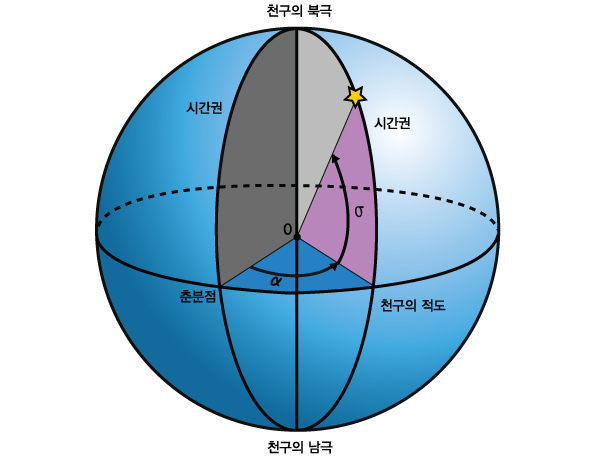
시간권은 천구의 북극과 남극을 있는 원들입니다. 지구의 경도를 나누는 경선들을 천구에 적용한 것이라 생각하면 됩니다.

두 좌표계에 대하여 살펴봤습니다. 위 내용은 다음과 같이 요약이 가능합니다.

  • 지평좌표계는 관측자의 북점으로부터의 (방위각, 고도)를 통하여 별의 위치를 계산
  • 적도좌표계는 천구의 춘분점으로부터의 (적경, 적위)를 통하여 별의 위치를 계산

좌표계 변환

앞서 살펴봤던 HYG-Database에서는 고정된 적위(RA), 적경(DEC)값을 얻을 수 있습니다. 하지만 우리가 있는 곳에서 실제로 어떻게 보이는지는 방위각, 고도 정보가 없으면 알 수 없습니다. 우리가 실제 접속하는 위치에서 보이는 밤하늘을 보여주기 위해서는, 적도좌표계의 값들을 지평좌표계의 값으로 변환해주어야 합니다.

적도좌표계를 지평좌표계로 변환하는 변환식은 해당 문서를 참고하였습니다.

좌표계 변환 (Above link)

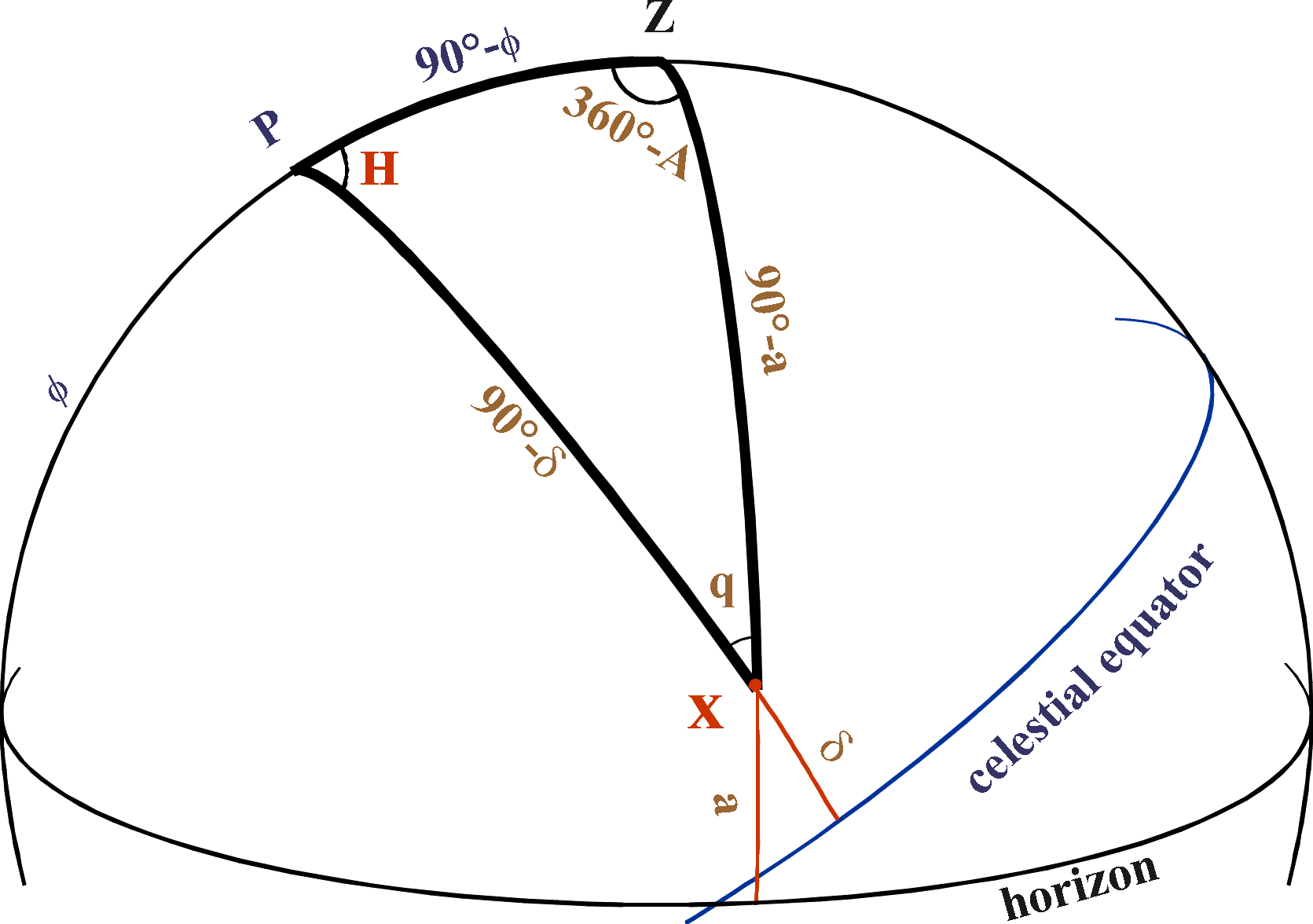
해당 그림이 핵심인데, 천구와 관측지의 지평선을 겹친 후 sin rule과 cosine rule을 이용하여 적도좌표계를 지평좌표계로 변환할 수 있습니다. 자세한 내용은 이 글에서는 생략합니다. 각각의 기호는 다음과 같습니다.

  • Z : 천정
  • P : 천구의 북극
  • X : 천체
  • H : 시각(= LST(항성시) - 천체의 적경)
  • δ : 천체의 적위
  • φ : 관측자의 위도
  • a : 천체의 고도
  • A : 천체의 방위각

를 의미합니다.

항성시

위 그림에서는 항성시에 대한 언급이 있는데, 아직 항성시를 정의하지 못했습니다. 항성시는 지구가 한 바퀴 자전해서 똑같은 별을 같은 방향에서 보게 되는데 걸리는 시간입니다. 태양시는 그 항성이 태양이라는 것을 빼면 다른 점이 거의 없습니다.

항성시를 사용하는 이유는 지구의 공전때문인데, 태양시보다 항성시를 쓰면 더 정확하게 적도좌표계를 지평좌표계로 변환할 수 있습니다. 현재 시간을 항성시로 변환하는 변환공식은 검색하면 여러 버전이 나오지만 단순한 버전을 선택하여 스크립트를 작성하였습니다.

변환 공식

이제 공식에 나오는 모든 변수를 정의했습니다. (적경, 적위)를 (위도, 경도, 항성시)를 이용하여 (방위각, 고도)로 변환하는 공식은 다음고 같습니다.

$$sin(a) = sin(\delta)sin(\phi) + cos(\delta)cos(\phi)cos(H) \\
tan(A) = \frac{sin(H)}{cos(H)sin(\phi)-tan(\delta)cos(\phi)}$$

해당 내용을 이용해서 작성한 스크립트와 테스트는 다음과 같습니다.

coordinate.js

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
// Thx to Suho Lee for nice reference.

const r2d = rad => rad * 180 / Math.PI;
const d2r = degree => degree * Math.PI / 180;

// getGeographic : ip -> {lat, long}
const getLocalGeographic = async () => {
    const endpoint = `http://ip-api.com/json/`
    const base = {lat: 37.582474, long: 127.027560};

    await fetch(endpoint)
    .then(res => this.geography = res.json())
    .catch(err => this.geography = base);

    return await this.geography;
};

// getLocalSidereal : long -> LST
const getLocalSidereal = (long) => {
    const now = new Date();
    const from2020 = new Date('2020/01/01');

    const offset = 
    (now.getTime() - from2020.getTime()) 
    / 1000.0 / 60.0 / 60.0 / 24.0;

    // Ignore err between UT1 and UTC,
    // since it's tiny.
    const UT1 = 
    now.getUTCHours()
    + now.getUTCMinutes() / 60.0
    + now.getUTCSeconds() / 3600.0;

    /* 
    * Formula by U.S. Naval Observatory, 2020
    */
    const GST = 
    (6.6090775
    + 0.0657098246 * offset
    + 1.00273791 * UT1)
    % 24;

    // GST = LST + long(converted to hours)
    const LST = (GST + long / 15.0) % 24;

    return LST;
};

// equatorialToHorizontal : lat -> LST -> star -> {az, alt}
const equatorialToHorizontal = (lat, LST, star) =>{
    /*
    * ra : hour
    * dec : -90 ~ +90
    * lat : -90 ~ +90
    * LST : hour
    * az : 360
    * alt : -90 ~ +90
    * HA : 0 ~ 360
    */

    const ra = star.getAttribute('ra');
    const dec = star.getAttribute('dec');

    // Convert HA to angle.
    const HA = (LST - ra) * 15 % 360;

    // For readability.
    const {sin, cos, tan, asin, acos, atan2} = Math;

    const Altitude = r2d(asin(
        sin(d2r(dec)) * sin(d2r(lat))
        + cos(d2r(dec)) * cos(d2r(lat)) * cos(d2r(HA))
    ));

    const Azimuth = r2d(atan2(
        sin(d2r(HA)),
        cos(d2r(HA)) * sin(d2r(lat)) - tan(d2r(dec)) * cos(d2r(lat))
    )) + 180

    const realAz = 300 + 0.20 * 10 / 6;
    const realAlt = 8 + 0.30 * 10 / 6;

    star.setAttribute('az', Azimuth);
    star.setAttribute('alt', Altitude);

    return {Azimuth, Altitude};
};


debug.js

잘 구현되었는지 테스트하기 위하여 테스트 코드를 다음과 같이 수정해줍시다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// For test
const getAlpheratz = () => {
    const sun = document.getElementsByTagName("star")[1];
    return sun;
}


init()
.then(async (stars) => await (load(stars)))
.then(async (stars) => await (projectTest(stars)))
.then(async () => this.geo = await getLocalGeographic())
.then(async () => this.LST = getLocalSidereal(this.geo.lon))
.then(async () => equatorialToHorizontal(this.geo.lat, this.LST, getAlpheratz()))
.then(async (azalt) => console.log(azalt))
.catch(err => console.log(err));

수정된 코드에서

1
2
3
4
await getLocalGeographic())
.then(async () => this.LST = getLocalSidereal(this.geo.lon))
.then(async () => equatorialToHorizontal(this.geo.lat, this.LST, getAlpheratz()))
.then(async (azalt) => console.log(azalt))

부분에서 나온 azalt값이 스텔라리움과 비교했을 때 비슷하면 구현이 성공한 것입니다.

결과

테스트 결과

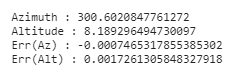
성공적으로 구현된 것을 확인할 수 있습니다.

다음 챕터에서는 투영을 구현합니다.
지평좌표계 적도좌표계 좌표계변환
prev: next: